In this tutorial we will be learning how to use Matrix Elimination to solve a linear system. Matrix Elimination is one of many techniques that can be used to solve systems of linear equation.
Here is an sample equation with solution
3x-5y+z=-23
-2x+3y-3z=19
4x+5z=-18
Step 1: Write the equation in Augmented Matrix.
Step 2: Use rows one and two to create the first in row two and we need to multiply row one by 2 and row two by 3 → 2R1 + 3R2 = R2
Step 3: Use rows one and three to create the second zero in row three and we need to multiply row one by -4 and row three by 3 → –4R1 + 3R3 = R3
Step 4: Use rows two and three to create the final zero in row three and we need to multiply row two by 20 and row three by 1 → 20R2 + R3 = R3
Step 5: To find the values of x, y, and z we want to use back substitution.
Using row three: –129z = 258
z = –2
Using row two: –y – 7z = 11
–y – 7(–2) = 11 put z=-2 and
–y + 14 = 11 solve for y
–y = –3
y = 3
Using row one: 3x – 5y + z = –23
3x – 5(3) + (–2) = –23
3x – 17 = –23 put z=-2, y=3
3x = –6 and solve x
x = –2
Program:
#include<stdio.h>
int main()
{
int i,j,r,n;
double a[15][15][15],x[15],sum=0;
printf("\n Enter the order of matrix :");
scanf("%d",&n);
printf("\n Enter the elements of the augmented matrix row-wise :\n\n");
for(i=0;i<n;i++)
{
for(j=0;j<n+1;j++)
{
printf("a[%d][%d]:",i+1,j+1);
scanf("%lf",&a[i][j][0]);
}
}
// Here is loop for the generation of upper triangular matrix
for(r=0;r<=n-1;r++)
{
for(i=r+1;i<=n-1;i++)
{
for(j=r+1;j<=n;j++)
{
a[i][j][r+1] = a[i][j][r] - a[r][j][r]*a[i][r][r]/a[r][r][r];
}
}
}
x[n]=a[n-1][n][n-1]/a[n-1][n-1][n-1];
// Here is loop for backward substitution
for(i=1;i<=n-1;i++)
{
sum=a[n-i-1][n][n-i-1];
for(j=1;j<=i;j++)
{
sum = sum - a[n-i-1][n-j][n-i-1] * x[n-j+1];
}
x[n-i]=sum/a[n-i-1][n-i-1][n-i-1];
}
printf("\n The solution is :\n");
for(i=0;i<=n-1;i++)
{
printf("\n x%d= %13.8lf\t",i+1,x[i+1]);
}
return 0;
}



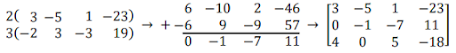





Thanks bro
ReplyDeletePost a Comment